Método de la secante
El método de la secante es un algoritmo de búsqueda de raíces que utiliza una sucesión de raíces de líneas secantes para aproximarse mejor a la raíz de una función f.
Esta página existe gracias a los esfuerzos de las siguientes personas:
 | Timur
|
 | Juan Manuel Gimenez
|
Este contenido está bajo licencia de Creative Commons Attribution/Share-Alike License 3.0 (Unported). Esto significa que puedes redistribuirlo o modificar su contenido en forma libre bajo las mismas condiciones de licencia y debes mantener la atribución del mismo al autor original de este trabajo colocando un hipervínculo en tu sitio web a este trabajo https://es.planetcalc.com/3707/. Así mismo, por favor no modifiques o alteres ninguna de las referencias al trabajo original (si hubiera alguna) que se encuentre en este contenido.
La breve descripción del método de la secante se encuentra debajo de la calculadora
Método de la secante
Método de la secante
El método de la secante puede pensarse como una aproximación al método de Newton con algunas diferencias menores, en el que la derivada se sustituye por la línea secante.
Utilizamos la raíz de la línea secante (el valor de x tal que y=0) como aproximación de la raíz para la función f.
Supongamos que tenemos los valores iniciales x0 y x1, con los valores de la función f(x0) y f(x1).
La línea secante tiene la ecuación
La raíz de la línea secante (donde у=0) por lo tanto
Esta es la relación de recurrencia para el método de la secante. La interpretación gráfica se puede ver a continuación.
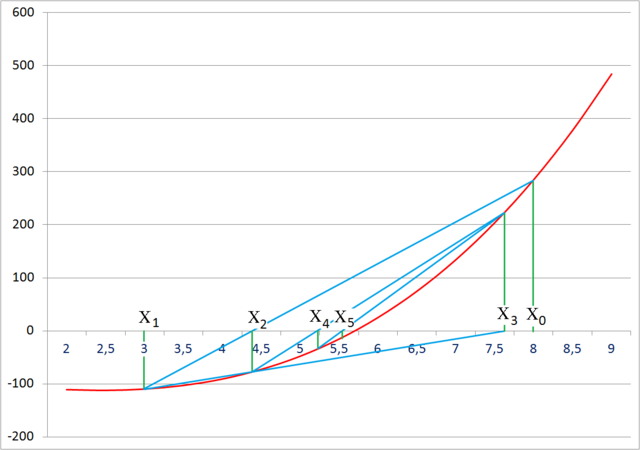
El método de la secante no requiere que la raíz permanezca entre corchetes como el método de bisección (véase más adelante), y por lo tanto no siempre converge.
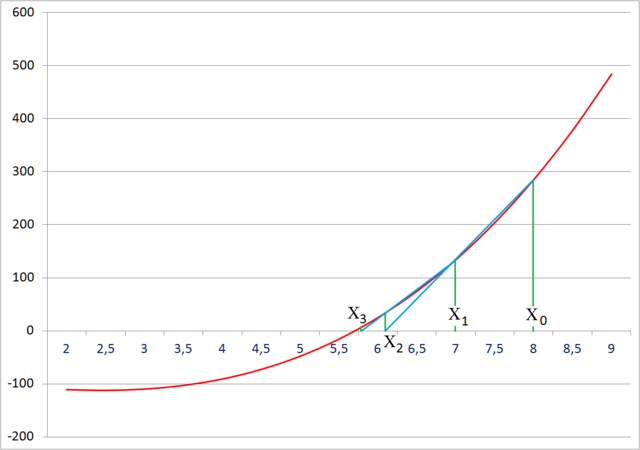
Como se puede ver en la relación de recurrencia, el método de la secante requiere dos valores iniciales, x0 y x1, que idealmente deberían ser elegidos para estar cerca de la raíz.
La condición de tolerancia puede ser cualquiera de las dos:
— el valor de la función es menor que ε.
— la diferencia entre dos хk posteriores es menor que ε.
Más: Método de la secante
Comentarios