Método de la falsa posición
El método de la falsa posición es un algoritmo de búsqueda de raíces que utiliza una sucesión de raíces de líneas secantes combinadas con el método de bisección para aproximar una raíz de una función f.
Una breve descripción del método de la falsa posición se puede encontrar debajo de la calculadora
Método de la falsa posición
El método de la falsa posición o método de la "regula falsi" es un algoritmo de búsqueda de raíces que combina características del método de bisección y el método de la secante.
Al igual que en el método de la secante, utilizamos la raíz de una línea secante (el valor de x tal que y=0) para calcular la siguiente aproximación de la raíz para la función f.
La derivación de la relación de recurrencia es la misma que en el método de la secante:
Supongamos que tenemos los valores iniciales x0 y x1, con los valores de la función f(x0) y f(x1).
La recta secante tiene la ecuación
Por lo tanto, la raíz de la recta secante (donde у=0) es
La fórmula anterior también se utiliza en el método de la secante, pero este método siempre conserva los dos últimos puntos calculados, mientras que el método de la falsa posición conserva dos puntos que siempre ponen entre paréntesis una raíz.
A continuación se puede ver una interpretación gráfica.
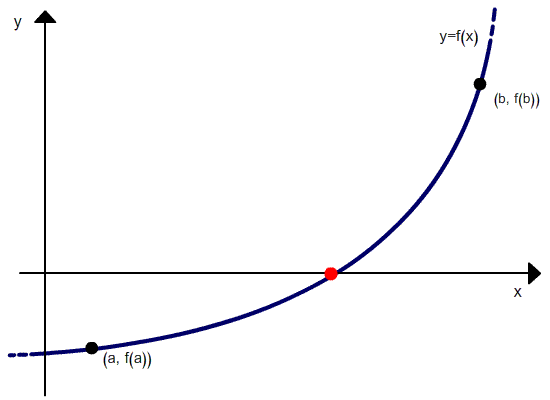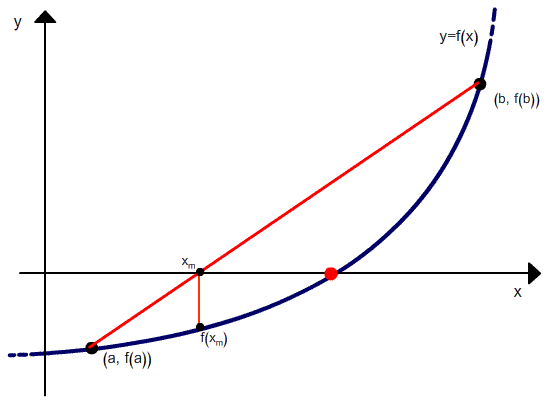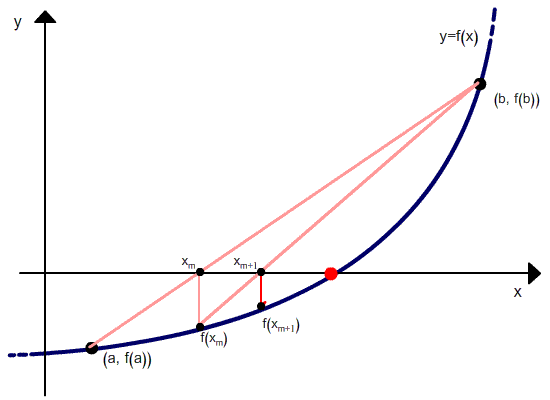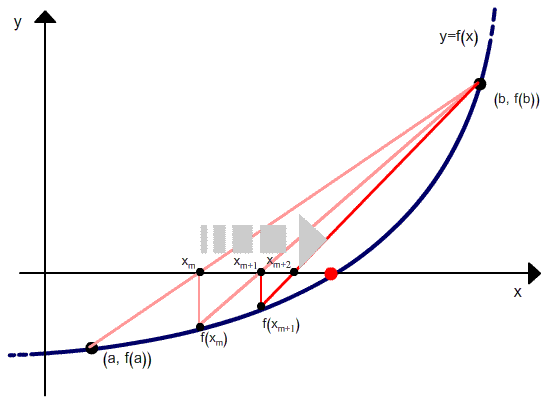
Como se puede ver en la relación de recurrencia, el método de la falsa posición requiere dos valores iniciales, x0 y x1, que deben poner entre paréntesis la raíz. Pero a diferencia del método de bisección, el ancho del paréntesis no tiende a cero con las iteraciones.
La condición de tolerancia puede ser cualquiera de las dos:
— el valor de la función es menor que ε.
— la diferencia entre dos хk posteriores es menor que ε. Nótese que esta es la diferencia entre dos xk posteriores calculados, no los puntos finales del intervalo.
Comentarios