Método de Newton
Esta calculadora en línea implementa el método de Newton (también conocido como el método de Newton-Raphson) para encontrar las raíces (o ceros) de una función de valor real.
Esta calculadora en línea implementa el método de Newton (también conocido como el método de Newton-Raphson) usando la calculadora de derivadas para obtener una forma analítica de la derivada de la función dada, porque este método lo requiere. La teoría para recordar los conceptos básicos del método se puede encontrar debajo de la calculadora.
Método de Newton–Raphson1
En el análisis numérico, el método de Newton (también conocido como el método de Newton-Raphson), llamado así por Isaac Newton y Joseph Raphson, es un método para encontrar sucesivamente mejores aproximaciones a las raíces (o ceros) de una función de valor real.
El método comienza con una función f definida sobre los números reales x, la derivada de la función f ′ y una estimación inicial x0 para una raíz de la función f. Si la función satisface las suposiciones hechas en la derivación de la fórmula y la estimación inicial está cerca, entonces una mejor aproximación x1 es
Geométricamente, (x1, 0) es la intersección del eje x y la tangente de la gráfica de f en (x0, f (x0)).
El proceso se repite como , hasta que se alcanza un valor suficientemente preciso.
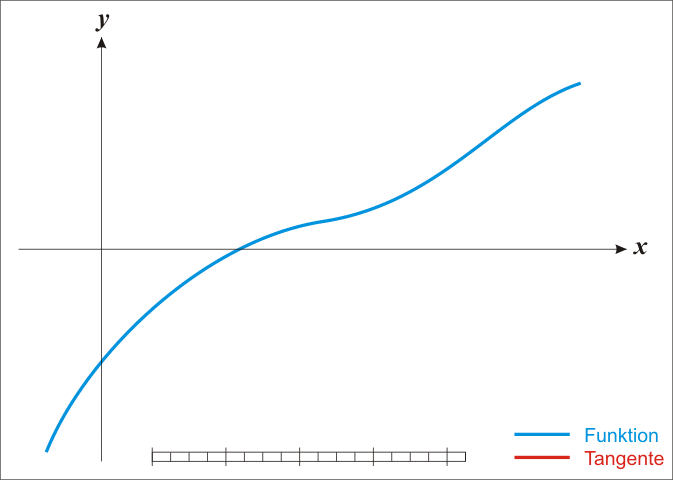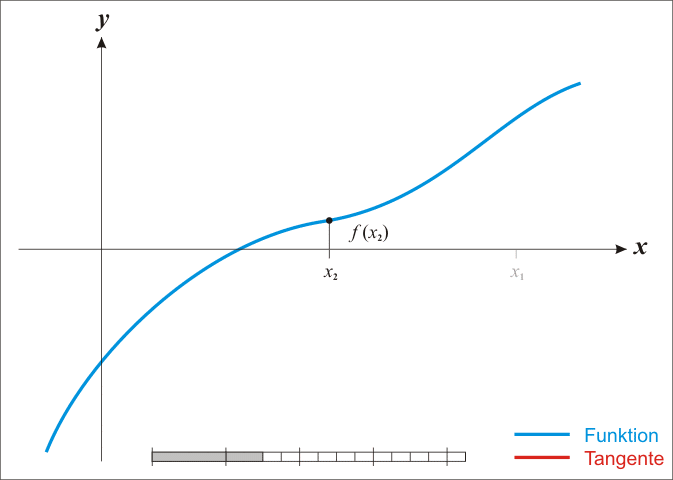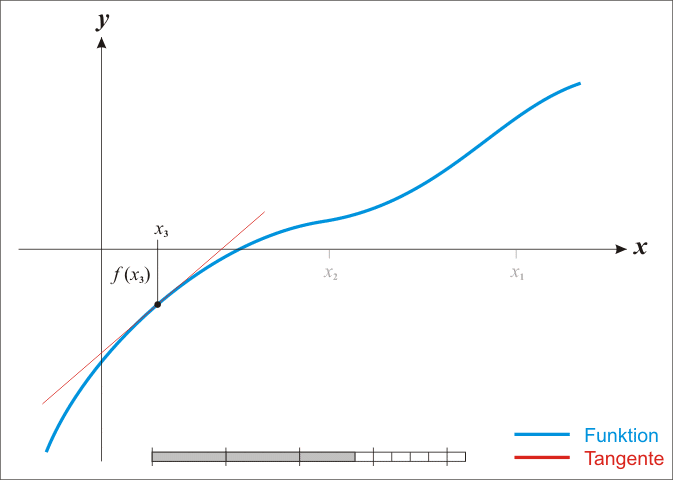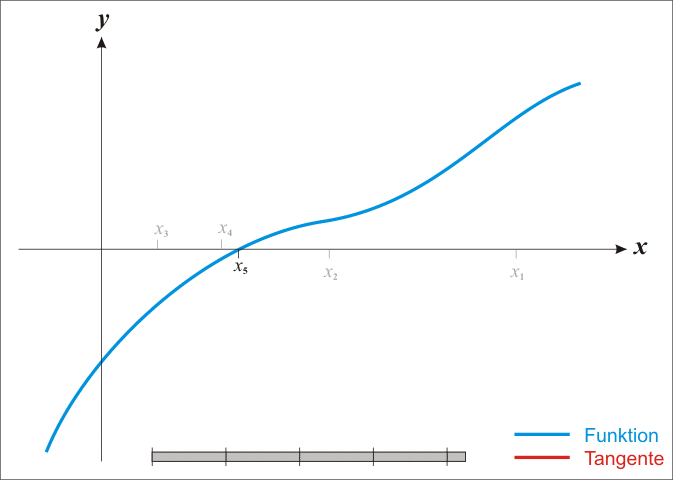
La idea del método es la siguiente: uno comienza con una conjetura inicial que está razonablemente cerca de la raíz verdadera, luego la función se aproxima por su línea tangente (que se puede calcular utilizando las herramientas de cálculo), y uno calcula la intersección de x de esta línea tangente (que se hace fácilmente con álgebra elemental). Esta intersección con X generalmente será una mejor aproximación a la raíz de la función que la suposición original, y el método puede ser iterado.
El método de Newton es una técnica extremadamente poderosa; en general, la convergencia es cuadrática: a medida que el método converge en la raíz, la diferencia entre la raíz y la aproximación es cuadrada (el número de dígitos exactos se duplica aproximadamente) en cada paso. Sin embargo, existen algunas dificultades con el método: dificultad para calcular la derivada de una función, falla del método para converger a la raíz, si no se cumplen los supuestos en la prueba de la convergencia cuadrática del método de Newton, la convergencia lenta para las raíces de multiplicidad mayor que 1.
Comentarios