PLANETCALC Calculadoras en línea

Iniciar Sesión
EstudioMatemáticaGeometría

Cortar un Círculo

Hay dos formas de cortar un círculo en partes iguales: cortes de segmento y cortes paralelos.

Esta página existe gracias a los esfuerzos de las siguientes personas:

Timur

Timur

Juan Manuel Gimenez

Juan Manuel Gimenez

Creado: 2021-06-13 18:57:39, Última actualización: 2021-06-15 17:14:32
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Este contenido está bajo licencia de Creative Commons Attribution/Share-Alike License 3.0 (Unported). Esto significa que puedes redistribuirlo o modificar su contenido en forma libre bajo las mismas condiciones de licencia y debes mantener la atribución del mismo al autor original de este trabajo colocando un hipervínculo en tu sitio web a este trabajo https://es.planetcalc.com/8943/. Así mismo, por favor no modifiques o alteres ninguna de las referencias al trabajo original (si hubiera alguna) que se encuentre en este contenido.

A continuación puedes encontrar dos calculadoras que calculan cómo cortar un círculo en partes iguales: de forma tradicional y no tradicional. Por la forma tradicional, asumo que se corta un círculo en segmentos, como se suele cortar una tarta o una pizza. Y por la forma no tradicional, asumo que se corta un círculo en partes verticales iguales con líneas paralelas o con cuerdas paralelas, si se quiere. Ambas calculadoras presentan un dibujo que ilustra el resultado. Y puede encontrar todas las fórmulas y cálculos en el artículo que aparece debajo de las calculadoras.

PLANETCALC, Cortar un círculo en segmentos iguales

Cortar un círculo en segmentos iguales

Dígitos después del punto decimal: 2
Ángulo de un Segmento
 
Longitud de un Arco de un Segmento
 
Longitud de la Cuerda de un Segmento
 

PLANETCALC, Cortar un círculo en partes iguales con Cortes Paralelos

Cortar un círculo en partes iguales con Cortes Paralelos

Dígitos después del punto decimal: 2
El archivo es muy grande; La ralentización del navegador puede ocurrir durante la carga y creación.

Cortar un Círculo en segmentos

Bien, usted necesita cortar un círculo en varios segmentos (incluso números no pares). Para ello, es necesario encontrar los parámetros de un segmento. Es una tarea sencilla:

  1. Encuentre el ángulo de un segmento en radianes dividiendo 2π (que representa 360 grados en radianes) entre un número de segmentos.

\alpha=\frac{2\pi}{N}

  1. Encuentre la longitud de un arco de un segmento multiplicando un radio por un ángulo de un segmento en radianes.

a=\alpha R

  1. Encuentre la longitud de una cuerda de un segmento utilizando la ley de los cosenos (una cuerda es la base del triángulo isósceles, con dos radios como catetos y el ángulo del segmento como ángulo del vértice).

c=R^2+R^2-2RR \cos \alpha

Esto define completamente todos los segmentos iguales N.

Cortar un Círculo con Cortes Paralelos

Esta forma es más interesante. Para simplificar, consideraré la mitad de un círculo ya que es simétrico.

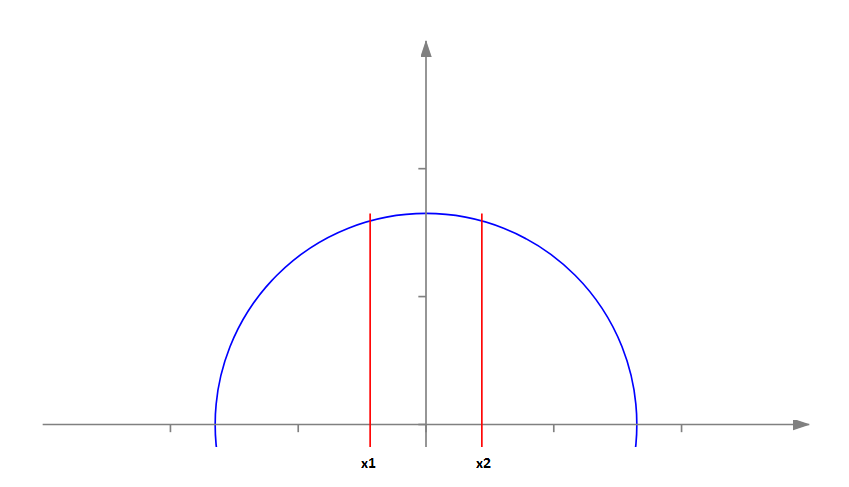
Cortar un Círculo en Tres Partes con Dos Líneas Paralelas
Cortar un Círculo en Tres Partes con Dos Líneas Paralelas

Vamos a cortarlo con cortes verticales. En este caso, tenemos que encontrar las coordenadas x de las cuerdas paralelas, que deberían dividir nuestro círculo en partes de igual área. (véanse los puntos x1 y x2 en la imagen anterior). Vamos a derivar la fórmula general para el área de un corte izquierdo.

Nuestro semicírculo puede pensarse como una función y=f(x), donde x - es la coordenada a lo largo del eje de abscisas, e y es la función igual al valor del punto correspondiente del semicírculo.

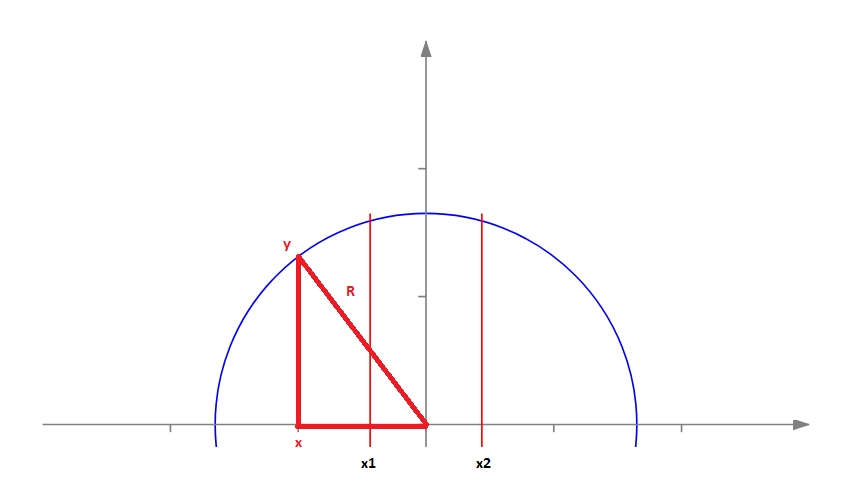
y=f(x)
y=f(x)

Utilizando el teorema de Pitágoras, la función y es

y=\sqrt{R^2 - x^2}}

Para encontrar el área de un corte a la izquierda, hay que integrar esta función desde -R hasta x. La antiderivada de nuestra función es :

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+C

Tenemos que encontrar el valor de la constante. Obviamente, en el punto donde x es igual a -R el área debe ser cero. Si introducimos -R en lugar de x en la fórmula anterior, obtenemos

F(-R)=-\frac{\pi R^2}{4}+C=0, por lo que

C=\frac{\pi R^2}{4}

Nuestra integral final es

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}

¿Ahora cómo encontramos la x del primer corte? Sabemos que el área que debemos obtener - la enésima parte del área total (nótese el semicírculo)

S=\frac{\frac{\pi R^2}{2}}{N}=\frac{\pi R^2}{2N}

Así, podemos equiparar

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}=\frac{\pi R^2}{2N}

Lo que nos da

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}-\frac{\pi R^2}{2N}=0

Esta es una ecuación trascendental, y necesitamos utilizar métodos numéricos para resolverla, por ejemplo, Método de bisección o Método de Newton. Aquí he utilizado el método de Newton.

Los siguientes puntos de corte se pueden encontrar con el mismo enfoque. Tenemos que cortar dos veces más para el segundo punto S_2=2\frac{\pi R^2}{2N}, tres veces más para el tercer punto S_3=3\frac{\pi R^2}{2N} y así sucesivamente.

Entonces podemos encontrar todos los demás parámetros, como la longitud de la cuerda, utilizando las coordenadas del punto.

URL copiada al portapapeles

Calculadoras similares

 #círculo #geometría ángulo arco área círculo corte cuerda Geometría paralelo sector segmento
PLANETCALC, Cortar un Círculo
Timur2021-06-15 17:14:32

Comentarios