Encontrar la intersección de dos círculos
Esta calculadora en línea encuentra los puntos de intersección de dos círculos dado el punto central y el radio de cada círculo. También los traza en la gráfica.
Esta página existe gracias a los esfuerzos de las siguientes personas:
 | Timur
|
 | Juan Manuel Gimenez
|
Para utilizar la calculadora, introduzca las coordenadas x e y de un centro y un radio de cada círculo.
Debajo de la calculadora se puede encontrar un poco de teoría.
Intersección de dos círculos
Primer círculo
Segundo círculo
Intersección de círculos
La tarea es relativamente fácil, pero debemos tener en cuenta los casos extremos - por lo tanto debemos empezar por calcular la distancia cartesiana d entre dos puntos de centro, y comprobar los casos extremos comparando d con los radios r1 y r2.
Aquí están los casos posibles (la distancia entre centros se muestra en rojo):
| Caso | Descripción | Regla |
|---|---|---|
| Caso trivial: las circunferencias son coincidentes (o es la misma circunferencia) | ||
 |
Los círculos están separados | |
 |
Un círculo está contenido dentro del otro | |
 |
Dos puntos de intersección | Se tienen uno o dos puntos de intersección si no se aplican todas las reglas de los casos extremos anteriores |
 |
Un punto de intersección | El caso trivial de dos puntos de intersección |
Así que, si no es un caso extremo, para encontrar los dos puntos de intersección, la calculadora utiliza las siguientes fórmulas (en su mayoría deducidas con el teorema de Pitágoras), ilustradas con el gráfico de abajo:
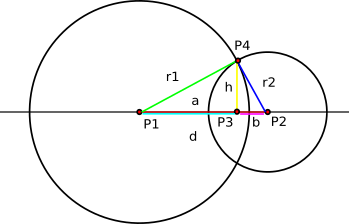
La primera calculadora encuentra el segmento a
y luego el segmento h
Para encontrar el punto P3, la calculadora utiliza la siguiente fórmula (en forma vectorial):
Y por último, para obtener un par de puntos en caso de que dos puntos se crucen, la calculadora utiliza estas ecuaciones:
Primer punto:
Segundo punto:
Observe los signos opuestos antes del segundo sumando.
Para más información, puede consultar a la intersección círculo-círculo y círculos y esferas.
Comentarios