Sistemas de coordenadas 3d
Transforma coordenadas 3D de/a sistemas de coordenadas cartesianas, cilíndricas y esféricas.
Este contenido está bajo licencia de Creative Commons Attribution/Share-Alike License 3.0 (Unported). Esto significa que puedes redistribuirlo o modificar su contenido en forma libre bajo las mismas condiciones de licencia y debes mantener la atribución del mismo al autor original de este trabajo colocando un hipervínculo en tu sitio web a este trabajo https://es.planetcalc.com/7952/. Así mismo, por favor no modifiques o alteres ninguna de las referencias al trabajo original (si hubiera alguna) que se encuentre en este contenido.
Esta calculadora está diseñada para la transformación de coordenadas de/a los siguientes sistemas de coordenadas 3d:
- Cartesiano
- Cilíndrico
- Esférico
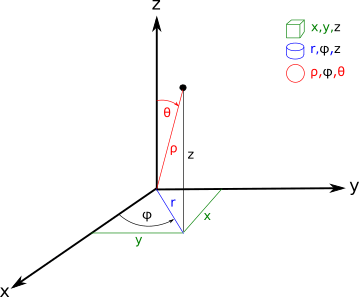
Sistemas de coordenadas cartesianas, cilíndricas y esféricas
Sistema de Coordenadas Cartesianas
En el sistema de coordenadas cartesianas se puede definir un punto con 3 números reales: x, y, z. Cada número corresponde a la distancia mínima con signo a lo largo de uno de los ejes (x, y o z) entre el punto y el plano, formado por los dos ejes restantes. La coordenada es negativa si el punto está detrás del origen del sistema de coordenadas.
Sistema de coordenadas cilíndricas
Este sistema de coordenadas define un punto en el espacio 3d con radio r, ángulo de acimut φ y altura z. La altura z corresponde directamente a la coordenada z en el sistema de coordenadas cartesianas. Radio r - es un número positivo, la distancia más corta entre el punto y el eje z. El ángulo de acimut φ es un valor de ángulo en el rango 0. 360 es un ángulo entre el semieje positivo xy, el radio desde el origen hasta la perpendicular, desde el punto hasta el plano XY.
Sistema de coordenadas esféricas
Este sistema define un punto en el espacio 3d con 3 valores reales: radio ρ, ángulo de acimut φ y ángulo polar θ. El ángulo de acimut φ es el mismo que el ángulo de acimut en el sistema de coordenadas cilíndricas. Radio ρ - es una distancia entre el origen del sistema de coordenadas y el punto. El semieje positivo z y el radio desde el origen hasta el punto forman el ángulo polar θ.
Fórmulas de transformación de coordenadas cartesianas:
Radio en sistema cilíndrico:
Radius en sistema esférico:
Ángulo de Acimut:
, ver Arco tangente de dos argumentos
Ángulo Polar:
Fórmulas de conversión de coordenadas cilíndricas:
A coordenadas cartesianas:
,
Radio en sistema de coordenadas esféricas:
Ángulo polar:
, ver Arco tangente de dos argumentos
Fórmulas de transformación de coordenadas esféricas
Coordenadas cartesianas:
,
,
Radio en sistema cilíndrico:
Calculadoras similares
- • Sistemas de coordenadas cartesianas y polares de dos dimensiones
- • Área de un triángulo a partir de sus coordenadas
- • Valores del triángulo por coordenadas de los vértices
- • Área de un rectángulo por coordenadas
- • Ecuación de una línea que pasa por dos puntos en 3d
- • Sección Geometría ( 212 calculadoras )
Comentarios