Puntuación Z a partir del valor P
Esta calculadora en línea calcula la puntuación z a partir del valor p
Esta calculadora en línea calcula la puntuación z a partir del valor p. Por supuesto, hay algunos valores conocidos, como todos (bueno, no todos en realidad) saben que la puntuación z para el nivel de significación de 0.05 es aproximadamente 1.64. Sin embargo, la calculadora que se muestra a continuación puede calcular la puntuación z para un valor p arbitrario. No es tan difícil, si usted puede calcular la inversa de CDF (función de distribución acumulativa) para la distribución normal estándar. Y eso es posible gracias a la excelente Librería jStat.
Ahora, permítame darle un par de ilustraciones de cómo funciona para diferentes hipótesis.
Evento de cola izquierda
Para el evento de cola izquierda, el valor p es la probabilidad de obtener un resultado igual o menor que el observado x. En este caso, el valor p es el valor de la función de distribución acumulativa de x, como se muestra en la imagen siguiente.
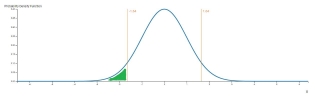
Para averiguar la puntuación z, sólo necesitamos obtener el inverso del CDF del valor p.
Evento de cola derecha
Para el evento de cola derecha, el valor p es la probabilidad de obtener un resultado igual o mayor que el observado x. En este caso, el valor p es el valor de una función de distribución acumulativa menor de x, como se muestra en la imagen siguiente.
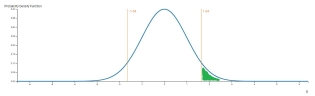
Para averiguar la puntuación z, sólo necesitamos obtener el inverso del CDF de un valor p menor.
Evento de doble cola
Para el evento de doble cola, el valor p es la doble probabilidad del "menor" de ambos. Conociendo sólo el valor p, asumimos que estamos hablando de valores x simétricos. En este caso, el valor p puede ser encontrado al duplicar el CDF de x de la cola izquierda, como se muestra en la imagen de abajo.
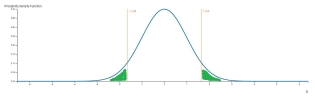
Para averiguar la puntuación z, sólo necesitamos obtener el inverso del CDF del valor p dividido por 2. Observe que en este caso la calculadora de abajo muestra el módulo de la puntuación Z.
Calculadoras similares
- • Estadísticas de PlanetCalc
- • Distribución geométrica. Función de densidad de probabilidad, función de distribución acumulativa, media y varianza
- • Distribución normal
- • Probabilidad de un número determinado de éxitos en varios ensayos de Bernoulli
- • Simulador de probabilidad de urna
- • Sección Estadísticas ( 3 calculadoras )
Comentarios