Volumen de un tanque cilíndrico inclinado
Calcula el volumen de un tanque cilíndrico inclinado a cierto ángulo. Para realizar el cálculo debes ingresar el tamaño del tanque, ángulo y nivel de líquido.
Para realizar el cálculo debes ingresar el tamaño del tanque, ángulo y nivel de líquido.
Medición del nivel del líquido
Debes medir el nivel de líquido en la línea media del tanque perpendicular al fondo del tanque. (ver la imagen). Puedes medir el nivel del líquido a cualquier distancia de la base (Si lo haces, debes ingresar la distancia en un parámetro especial).
De forma alternativa, puedes inclinar el tanque para crear un nivel cero de líquido en la base superior, en este caso debes sólo medir el ángulo de inclinación.
Debajo de la calculadora se encuentran detalles del cálculo y fórmulas.
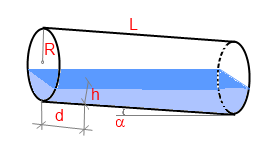
No puedo encontrar una solución ya hecha para calcular el volumen de un líquido en un cilindro inclinado, así que derive la fórmula de esta forma:
donde - como el ángulo del segmento depende de la longitud x del cilindro,
se puede derivar como:
donde
a - ángulo de inclinación,
h0 - nivel de líquido en la parte superior
Si substituimos esta expresión en la fórmula, obtenemos:
donde
Si tomamos la integral obtenemos la solución:
donde
Comentarios