Calculadora en línea: Valores del triángulo por coordenadas de los vértices

Valores del triángulo por coordenadas de los vértices

Esta calculadora en línea calcula un conjunto de valores del triángulo: longitud de los lados, ángulos, perímetro y área por las coordenadas de sus vértices

Esta calculadora en línea está diseñada para calcular rápidamente una serie de características de un triángulo a partir de las coordenadas de sus vértices. Se introducen las coordenadas de los vértices A, B y C. La calculadora calcula los siguientes valores a partir de las coordenadas:

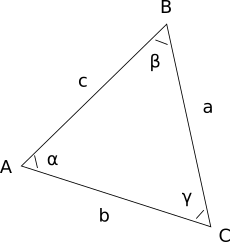
la longitud del lado a - el lado opuesto al vértice A
la longitud del lado b - el lado opuesto al vértice B
la longitud del lado c - el lado opuesto al vértice C
el valor del ángulo α en el vértice A
el valor del ángulo β en el vértice B
el valor del ángulo γ en el vértice C
el perímetro del triángulo
el área del triángulo

Si necesita algo más, escriba en los comentarios, lo añadiremos. Las fórmulas para calcular los valores de los triángulos se describen en la calculadora.

Valores del triángulo por coordenadas de los vértices

Vértice A

x₁

y₁

Vértice B

x₂

y₂

Vértice C

x₃

y₃

Cálculo preciso

Dígitos después del punto decimal: 2

Lado a

Lado b

Lado c

Ángulo α

Ángulo β

Ángulo γ

Perímetro

Área

Calcular un triángulo por las coordenadas de los vértices

Las longitudes de los lados se encuentran mediante la fórmula para calcular la distancia entre puntos en coordenadas cartesianas
$c = l_ {AB} = \ sqrt {(x_2-x_1) ^ 2 + (y_2-y_1) ^ 2}$

Los ángulos provienen de las fórmulas del producto punto de los vectores en los vértices.
$\mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\ \|\mathbf {b} \|\cos \gamma$

El perímetro se determina simplemente sumando las longitudes de los lados.
$P = a + b + c$

El área de un triángulo se encuentra a través del determinante
$S=\pm \frac{1}{2} \left| \begin{matrix} x_1 - x_3 & y_1 - y_3 \\ x_2 - x_3 & y_2 - y_3 \end{matrix} \right|=\pm \frac{1}{2} \left( (x_1 - x_3)(y_2 - y_3) - (y_1 - y_3)(x_2 - x_3) \right)$

PLANETCALC Calculadoras en línea

Valores del triángulo por coordenadas de los vértices

Esta página existe gracias a los esfuerzos de las siguientes personas:

Timur

Juan Manuel Gimenez

Valores del triángulo por coordenadas de los vértices

Vértice A

Vértice B

Vértice C

Calcular un triángulo por las coordenadas de los vértices

Calculadoras similares

Comentarios

PLANETCALC Calculadoras en línea

Valores del triángulo por coordenadas de los vértices

Vértice A

Vértice B

Vértice C

Calcular un triángulo por las coordenadas de los vértices

Calculadoras similares

Comentarios

Comparte esta página