Calculadora en espiral
Esta calculadora en línea determina las dimensiones desconocidas de la espiral de Arquímedes a partir de las dimensiones conocidas. Las dimensiones de la espiral incluyen: diámetro exterior, diámetro interior, distancia de separación (distancia entre brazos, espesor), longitud de la espiral y número de giros.
Esta es una calculadora universal para la espiral de Arquímedes.

Tenemos cinco dimensiones de la espiral: diámetro exterior - D, diámetro interior - d, espesor, distancia de separación o distancia entre los brazos - t, longitud de la espiral - L, número de giros - n. Estas dimensiones están relacionadas (ver fórmulas debajo de la calculadora), y puede calcular dos de ellas si conoce las otras tres.
Podemos ver espirales en la vida cotidiana en cualquier objeto que esté en forma de rollo: rollos de papel, cintas, películas, etc. Puede averiguar fácilmente algunas de las dimensiones de estos objetos, como los diámetros y el espesor, o el número de giros, y, con la calculadora que aparece a continuación, calcular las que faltan. Por ejemplo, puede calcular la longitud del rollo a partir de los diámetros interior y exterior y el espesor del rollo o el número de giros. También se puede resolver un problema inverso (cuando se conoce la longitud del rollo): calcular el espesor y el número de giros a partir de la longitud del rollo y ambos diámetros. La teoría y las fórmulas, como siempre, se encuentran debajo de la calculadora.
¡Por favor, tenga cuidado con el control de las unidades cuando introduzca las dimensiones conocidas! 20 metros no son lo mismo que 20 milímetros...
Espiral de Arquímedes
La espiral de Arquímedes (también conocida como espiral aritmética) es una espiral que corresponde a las localizaciones en el tiempo de un punto M que se aleja de un punto central O con velocidad constante a lo largo de una línea OA que gira alrededor del punto central O con velocidad angular constante.

Si denotamos la distancia de O a M como ρ, y el ángulo de rotación como φ, entonces podemos describir una espiral con la ecuación polar:
,
donde k es el parámetro de tamaño, que equivale al cambio de distancia cuando el ángulo gira 1 radián. Después de un giro (un ángulo aumenta en 2π), la distancia aumenta en 2πk.
Este aumento es la distancia entre dos brazos de una espiral, distancia de separación o espesor de la espiral. Podemos reescribir nuestra ecuación inicial utilizando a:
Como el espesor es constante, cuanto más se aleja el punto M del centro, más se parece la espiral al círculo.
Para derivar la fórmula de la longitud de la espiral, examinaremos el cambio de longitud infinitesimal.
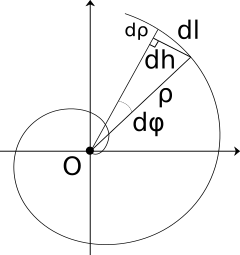
Un segmento infinitesimal de espiral dl puede considerarse como la hipotenusa del triángulo dl, dρ y dh. Por lo tanto:
Un segmento infinitesimal de espiral dh puede sustituirse por un segmento infinitesimal de una circunferencia de radio ρ; por tanto, su longitud es ρdφ.
Utilizando la ecuación polar de una espiral, podemos sustituir ρ por kφ, y dρ por kdφ
Ahora tenemos la dependencia de la longitud dl del ángulo dφ. Para averiguar la longitud, tenemos que integrar desde el ángulo inicial hasta el ángulo final.
Resumiendo, la integral final es:
Si una espiral parte de un ángulo cero (desde el centro), la fórmula se simplifica:
Pero en la vida real, por supuesto, un rollo de material no parte del centro. Por lo general, tiene un manguito, de ahí el diámetro interior y el ángulo inicial. ¿Cómo se relacionan todos estos parámetros?
He aquí cómo se relaciona el número de giros n con los ángulos:
Y he aquí cómo se relacionan los diámetros con los ángulos (esto se deduce directamente de la ecuación polar espiral)
Todas estas son fórmulas que necesitamos para averiguar las dimensiones desconocidas por las conocidas. Sin embargo, hay que tener en cuenta que la ecuación de la longitud es trascendental, y la tarea inversa (encontrar las dimensiones desconocidas mientras la longitud está entre las dimensiones conocidas) requiere métodos numéricos. Esta calculadora utiliza el método de la secante.
Calculadoras similares
- • Espesor de pared de cañería
- • Relaciones entre la masa, la longitud, la anchura y la densidad del área (densidad de superficie) del tejido
- • Ángulo de rumbo y distancia entre los dos puntos de la loxodrómica (línea de rumbo).
- • Longitud de los lados de un triángulo
- • Longitud de los lados de un triángulo dado un lado y dos ángulos
Comentarios