Calculadora en línea: Radio de la Tierra según Latitud (WGS 84)

La calculadora de abajo calcula el radio de la Tierra a una latitud dada. De hecho, por supuesto, calcula el radio del elipsoide de referencia WGS 84 a una latitud dada, y si quiere un poco de recapitulación de la teoría, puede encontrarla debajo de la calculadora.

Radio de la Tierra según Latitud (WGS 84)

Latitud

′

″

Cálculo preciso

Dígitos después del punto decimal: 3

Radio (km)

Radio de la Tierra

Dado que la Tierra es estrecha en los polos y abultada en el ecuador, la geodesia representa la forma de la Tierra con un esferoide oblato. El esferoide oblato, o elipsoide oblato, es un elipsoide de revolución que se obtiene al girar una elipse alrededor de su eje más corto. Es la forma geométrica regular que más se aproxima a la forma de la Tierra. Un esferoide que describe la figura de la Tierra u otro cuerpo celeste se llama Elipsoide de referencia. El elipsoide de referencia para la Tierra se denomina elipsoide terrestre.

La superficie física de la Tierra es irregular. Puede ser aproximada por el geoide, que fue un concepto importante durante casi doscientos años de historia de la geodesia y la geofísica. Según Gauss, que lo describió por primera vez, es la "figura matemática de la Tierra", una superficie lisa pero muy irregular cuya forma es el resultado de la distribución desigual de la masa dentro y sobre la superficie terrestre. La superficie del geoide es irregular pero considerablemente más suave que la superficie física de la Tierra.

Debido a su relativa simplicidad, los elipsoides de referencia se utilizan como superficie preferida sobre la que se realizan los cálculos de la red geodésica y se definen las coordenadas de puntos como la latitud, la longitud y la elevación. Actualmente, el elipsoide de referencia más utilizado, y el que se usa en el contexto del Sistema de Posicionamiento Global, es el definido por WGS 84.

Dos magnitudes definen de forma única un elipsoide de revolución. En geodesia se utilizan varias convenciones para expresar las dos magnitudes, pero todas ellas son equivalentes y convertibles entre sí:

Radio ecuatorial a (llamado eje semimayor), y el radio polar b (llamado eje semimorfo);
a y excentricidad e;
a y el estrechamiento f.

WGS 84 define los parámetros del elipsoide como:
Eje semimayor a = 6378137,0 metros
Eje semimayor b = 6356752,3142 metros

El punto de la superficie del elipsoide puede definirse mediante la ecuación de la curva paramétrica
$(x,y)=(a \, cos(t), b \, sin(t))$

El radio se puede encontrar utilizando el teorema de Pitágoras
$R(t)^2 = a^2 cos^2(t) + b^2 sin^2(t)$

Sin embargo, el problema es que el ángulo t del ejemplo anterior es la latitud geocéntrica, y las coordenadas proporcionadas en datum geodésico, como WGS 84, son geodésicas. La latitud geodésica está determinada por el ángulo entre el plano ecuatorial y la normal al elipsoide. En cambio, la latitud geocéntrica se determina por el ángulo entre el plano ecuatorial y la línea que une el punto con el centro del elipsoide (véase la figura).

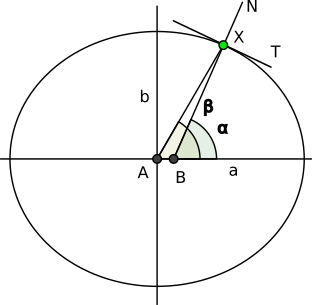
Por lo tanto, para encontrar el radio, necesitamos relacionar la latitud geodésica $\alpha$ a la latitud geocéntrica $\beta$ .

Partamos de la tangente de nuestra curva, que se puede obtener diferenciando la ecuación de la curva.
$(x,y)'=(\frac{dx}{dt}, \frac{dy}{dt}) = ( -a \, sin(t), b \, cos(t))$

Este es el vector que apunta a lo largo de la curva (a lo largo de la línea T en la figura).

Podemos girar 90 grados en el sentido de las agujas del reloj $(x,y) => (y, -x)$ y obtener el vector normal $(b \, cos(t), a \, sin(t))$ que apunta a la línea N.

El parámetro t es nuestro $\alpha$ . La pendiente del vector normal es también la tangente del ángulo $\beta$ . Por lo tanto
$tan(\beta)=\frac{a \, sin(\alpha)}{b \, cos(\alpha)}=\frac{a}{b}tan(\alpha)$
o
$tan(\alpha)=\frac{b}{a}tan(\beta)$

Utilizando las relaciones entre la tangente y el coseno
$1+tan^2(\alpha)=\frac{1}{cos^2(\alpha)} => cos^2(\alpha)=\frac{1}{1+tan^2(\alpha)}$
y entre la tangente y el seno
$1+cotan^2(\alpha)=\frac{1}{sin^2(\alpha)} => sin^2(\alpha)=\frac{1}{1+\frac{1}{tan^2(\alpha)}}=\frac{tan^2(\alpha)}{1+tan^2(\alpha)}$ ,
podemos reescribir la fórmula del radio como
$R^2 = a^2 \frac{1}{1+tan^2(\alpha)} + b^2 \frac{1}{1+\frac{1}{tan^2(\alpha)}} = \frac{a^2}{1+tan^2(\alpha)} + b^2 \frac{tan^2(\alpha)}{1+tan^2(\alpha)}$
y reemplazar la tangente de $\alpha$ con la expresión de la tangente de $\beta$
$R^2 = \frac{a^2}{1+\frac{b^2}{a^2}tan^2(\beta)} + b^2\frac{\frac{b^2}{a^2}tan^2(\beta)}{1+\frac{b^2}{a^2}tan^2(\beta)}=\frac{a^4+b^4tan^2(\beta)}{a^2+b^2tan^2(\beta)}$

Entonces, podemos simplificarla un poco
$R^2 =\frac{a^4+b^4tan^2(\beta)}{a^2+b^2tan^2(\beta)} = \frac{a^4cos^2(\beta)+b^4sin^2(\beta)}{a^2cos^2(\beta)+b^2sin^2(\beta)}= \frac{ (a^2cos(\beta))^2+(b^2sin(\beta))^2}{(a\,cos(\beta))^2+(b\,sin(\beta))^2}$

Y, finalmente, obtener la fórmula de Wikipedia

$R =\sqrt{\frac{ (a^2cos(\beta))^2+(b^2sin(\beta))^2}{(a\,cos(\beta))^2+(b\,sin(\beta))^2}}$

La calculadora anterior utiliza esta fórmula.

PLANETCALC Calculadoras en línea

Radio de la Tierra según Latitud (WGS 84)

Radio de la Tierra según Latitud (WGS 84)

Radio de la Tierra

Calculadoras similares

Comentarios

PLANETCALC Calculadoras en línea

Radio de la Tierra según Latitud (WGS 84)

Radio de la Tierra

Calculadoras similares

Comentarios

Comparte esta página