Capacitador en un circuito de corriente directa
Estas calculadoras en línea encuentran varios parámetros para cargar y descargar un capacitador utilizando el resistor.
Estas calculadoras en línea encuentran varios parámetros para cargar y descargar un capacitador utilizando el resistor. Las fórmulas utilizadas para los cálculos se encuentran debajo de las calculadoras.
Debajo se encuentra la imagen de un circuito eléctrico para cargar el capacitador con la fuente de poder.
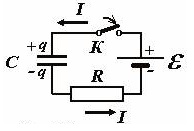
Luego que el switch K esté cerrado, la corriente directa comienza a cargar el capacitador.
De acuerdo a la ley de Ohm, la suma de los voltajes del capacitador y resistor es igual al voltaje de la fuente de poder.
La carga del capacitador y corriente dependen del tiempo. En el momento inicial, no hay carga en el capacitador, entonces la corriente es máxima, también la disipación de energía en el resistor.
Durante la carga, el voltaje del capacitador cambia de acuerdo a la siguiente ecuación
donde tau
es llamado Constante de tiempo. Como la carga es un proceso infinito, usualmente, un capacitador se considera totalmente cargado luego de 5 constantes de tiempo. Luego de este tiempo, el capacitador estará cargado a 99.2% de la fuente de voltaje.
Carga del capacitador
Energía del capacitador
Trabajo de la fuente de energía
Comentarios