Segmento circular
Puede calcular el área, longitud del arco, longitud de cuerda, altura y perímetro de un segmento circular a partir de su radio y ángulo.
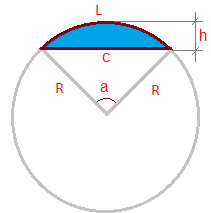
Segmento circular - es el área de un círculo que se "cortado" del resto de círculo por una secante (cuerda).
En la imagen:
L - longitud del arco
h- altura
c- cuerda
R- radio
a- ángulo
Si conoces el radio y ángulo puedes utilizar las siguientes fórmulas para calcular los demás parámetros del segmento:
Fórmulas para segmento circular
Área:
[1]
Longitud del arco:
Longitud de la cuerda:
Altura del segmento:
Pero si no conoces el radio o ángulo igual puedes calcular los parámetros del segmento a partir de la longitud de la cuerda y la altura del segmento:
Fórmula para el radio del segmento a partir de la cuerda y altura:
Luego, puedes calcular el ángulo del segmento utilizando la siguiente fórmula:
También puedes usar esta calculadora para obtener el área del segmento a partir de su radio y altura:
Esta calculadora evalúa el ángulo a partir de la siguiente fórmula:
Luego utiliza la fórmula [1] para calcular el área del segmento.
Comentarios