Cono
Un cono es una figura de tres dimensiones que tiene una base circular y un vértice.


Un cono oblicuo es un cono con un vértice que no está alineado con el centro de la base.
Un cono recto es un cono con un vértice que está directamente alineado encima del centro de la base. La base no tiene que ser circular.
El volumen de un cono recto es , donde
_ es el área de superficie de la base del cono.
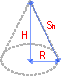
Cuando la base de un cono recto es un círculo, se llama cono circular recto.
Tal cono se caracteriza por el radio de la base y la altitud del cono, es decir, la distancia del vértice al centro de la base. De tal forma el volumen de un cono circular recto es
La altura de inclinación de tal cono es la longitud de una línea recta dibujada de cualquier punto del perímetro del cono al vértice.
Si el radio de la base es R y la altitud del cono es H, entonces la altura de inclinación es
Ahora podemos calcular el área total de superficie de un cono circular recto:
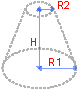

Un cono truncado es un cono en el cual el plano cortando la punta es paralelo a la base.
El volumen de un cono circular truncado es
El área de superficie de un cono circular truncado es
Comentarios